• 1500ms
  • 524288K

The beautiful values of the palace

Here is a square matrix of $n\times n$, each lattice has its value ($n$ must be odd), and the center value is $n\times n$ . Its spiral decline along the center of the square matrix (the way of spiral decline is shown in the following figure:)

img

img

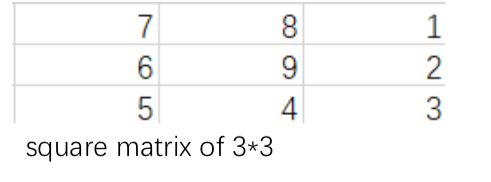
The grid in the lower left corner is (1,1) and the grid in the upper right corner is (n , n)

Now I can choose $m$ squares to build palaces, The beauty of each palace is equal to the digital sum of the value of the land which it is located. Such as (the land value is $123213$,the beautiful values of the palace located on it is $1+2+3+2+1+3=12$) ($666$ -> $18$) ($456$ ->$15$)

Next, we ask $p$ times to the sum of the beautiful values of the palace in the matrix where the lower left grid($x_1,y_1$), the upper right square ($x_2,y_2$).

Input

The first line has only one number $T$ .Representing $T$-group of test data ($T\le 5$)

The next line is three number: $n\ m\ p$

The $m$ lines follow, each line contains two integers the square of the palace ($x, y$)

The $p$ lines follow, each line contains four integers : the lower left grid ($x_1,y_1$) the upper right square ($x_2,y_2$)

Output

Next, $p_1+p_2…+p_T$ lines: Represent the answer in turn($n \le 10^6$)($m , p \le 10^5$)

样例输入

1
2
3
4
5
6
7
8
9
10
1
3 4 4
1 1
2 2
3 3
2 3
1 1 1 1
2 2 3 3
1 1 3 3
1 2 2 3

样例输出

1
2
3
4
5
18
23
17

题意

给定一个$n\times n$ 的矩阵，构造方法：从右上角顺时针旋转形成。然后给出 $m$ 个点，只有这 $m$ 个点的值有效，别的全部变为 $0$，然后有 $q$ 个查询，每次查询一个区域，求这个区域内的格子的权值和，一个格子的权值定义为这个格子数值的数位和。

解决方案

考虑用线段树离线处理（其实用主席树在线处理可能更好）。

按照 $x$ 轴去建立一棵线段树，线段树存的值是 $x$ 坐标在某一区间内的点的权值之和。我们先把所有的点，即包括有效点和查询点共 $m + 2q$ 个点，放在一个数组里，然后按照 $y$ 轴从小到大排序， $y$ 相同则按 $tag$ 排序。注意，点存入该数组时要加标记，要出入的点（即那 $m$ 个）$tag$ 为 $1$，查询的左下角的点 $tag$ 为 $0$，查询的右上角的点 $tag$ 为 $2$ ，为什么要这么标记呢？下面解释。

首先，我们顺序扫描这个数组

  • 碰到 $tag$ 为 $1$ 的点，则插入线段树。
  • $tag$ 为 $0$ 的点，则说明它是某一个查询的左下角的点，此时需要查询一次他和其对应的右上角点所夹的 $x$ 轴区间的值，存到ans数组里去，即 $ans[p[i].id] = query(l_1, l_2)$，$l_1$ 是当前点的 $x$ 坐标，$l_2$ 是其对应右上角点的 $x$ 坐标。
  • $tag$ 为 2 的点，则说明它是某个查询的右上角的点，此时也要进行一次查询，查询的区间同上，此时更新答案 $ans[p[i].id] = query(l_1, l_2) - ans[p[i].id]$

用这幅图来说明就是，用大的矩形减去那个小的矩形，即为答案。那为什么之前的 $tag$ 要那么安排呢？这里有一个细节要注意，我们减的时候，不能把左下角那个点所在的那一行也给减掉啊，所以在排序时，当 $y$ 相同时，左下角的点必须排在要插入的点之前，同理，右上角的点必须排在要插入的点之后。

至于如何 $O(1)$ 获取构造的矩阵中某个点的值，有公式，网上也有资料，大家可以自己推一下。

类似的思路，用主席树也可以很快的写出来。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn = 1e6 + 10;

struct node {
  int x, y, x1;
  int id, tag;
  bool operator<(const node& t) const {
    if (y == t.y) {
      return tag < t.tag;
    } else {
      return y < t.y;
    }
  }
} p[maxn];

ll tree[maxn << 2];
ll ans[maxn];
int n, m, q;

void update(int l, int r, int rt, int c, ll val) {
  if (l == r) {
    tree[rt] += val;
    return;
  }
  int m = (l + r) >> 1;
  if (c <= m) {
    update(l, m, rt << 1, c, val);
  } else {
    update(m + 1, r, rt << 1 | 1, c, val);
  }
  tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}

ll query(int l, int r, int tl, int tr, int rt) {
  if (l <= tl && r >= tr) {
    return tree[rt];
  }
  int tm = (tl + tr) >> 1;
  ll tmp = 0;
  if (l <= tm) {
    tmp += query(l, r, tl, tm, rt << 1);
  }
  if (r > tm) {
    tmp += query(l, r, tm + 1, tr, rt << 1 | 1);
  }
  return tmp;
}

ll ff(ll x, ll y) {
  x = n - x + 1;
  y = n - y + 1;
  ll r = 0;
  if (x <= y & x + y <= n + 1) {
    r = x;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + y - r;
  }
  if (x <= y & x + y >= n + 1) {
    r = n - y + 1;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + n - 2 * r + 1 + x - r;
  }
  if (x >= y & x + y >= n + 1) {
    r = n - x + 1;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + 3 * n - 6 * r + 3 - y +
           r;
  }
  if (x >= y & x + y <= n + 1) {
    r = y;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + 4 * n - 8 * r + 4 - x +
           r;
  }
  return 0;
}

ll f(ll x, ll y) {
  ll ans = ff(x, y);
  ll sum = 0;
  while (ans) {
    sum += ans % 10;
    ans /= 10;
  }
  return sum;
}

int main() {
  int T;
  scanf("%d", &T);
  while (T--) {
    memset(tree, 0, sizeof(tree));
    scanf("%d%d%d", &n, &m, &q);
    int tot = 0;
    while (m--) {
      scanf("%d%d", &p[tot].x, &p[tot].y);
      p[tot++].tag = 1;
    }
    for (int i = 0; i < q; i++) {
      scanf("%d%d", &p[tot].x, &p[tot].y);
      p[tot].id = p[tot + 1].id = i;
      p[tot++].tag = 0;
      scanf("%d%d", &p[tot].x, &p[tot].y);
      p[tot - 1].x1 = p[tot].x;
      p[tot].x1 = p[tot - 1].x;
      p[tot++].tag = 2;
    }
    sort(p, p + tot);
    for (int i = 0; i < tot; i++) {
      if (p[i].tag == 1) {
        update(1, n, 1, p[i].x, f(p[i].x, p[i].y));
      } else if (p[i].tag == 0) {
        int id = p[i].id;
        ans[id] = query(p[i].x, p[i].x1, 1, n, 1);
      } else {
        int id = p[i].id;
        ans[id] = query(p[i].x1, p[i].x, 1, n, 1) - ans[id];
      }
    }
    for (int i = 0; i < q; i++) {
      printf("%lld\n", ans[i]);
    }
  }
  return 0;
}

9.3更新

代码2

补上一个用主席树写的版本，在线查询，不用离线……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn = 1e6 + 10;

struct node {
  int lch, rch, sum;
};

struct point {
  int x, y;

  bool operator<(const point& t) const { return y < t.y; }
};

node tree[maxn * 40];
point p[maxn];
int root[maxn];
int tot;
int n;

void build(int l, int r, int& rt) {
  rt = tot++;
  tree[rt].sum = 0;
  if (l == r) {
    return;
  }
  int m = (l + r) >> 1;
  build(l, m, tree[rt].lch);
  build(m + 1, r, tree[rt].rch);
}

void update(int l, int r, int& rt, int pre, int c, int val) {
  rt = tot++;
  tree[rt] = tree[pre];
  tree[rt].sum += val;
  if (l == r) {
    return;
  }
  int m = (l + r) >> 1;
  if (c <= m) {
    update(l, m, tree[rt].lch, tree[pre].lch, c, val);
  } else {
    update(m + 1, r, tree[rt].rch, tree[pre].rch, c, val);
  }
}

int query(int tl, int tr, int rt, int pre, int l, int r) {
  if (l <= tl && r >= tr) {
    return tree[rt].sum - tree[pre].sum;
  }
  int tm = (tl + tr) >> 1;
  int sum = 0;
  if (l <= tm) {
    sum += query(tl, tm, tree[rt].lch, tree[pre].lch, l, r);
  }
  if (r > tm) {
    sum += query(tm + 1, tr, tree[rt].rch, tree[pre].rch, l, r);
  }
  return sum;
}

ll ff(int x, int y) {
  x = n - x + 1;
  y = n - y + 1;
  ll r = 0;
  if (x <= y & x + y <= n + 1) {
    r = x;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + y - r;
  }
  if (x <= y & x + y >= n + 1) {
    r = n - y + 1;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + n - 2 * r + 1 + x - r;
  }
  if (x >= y & x + y >= n + 1) {
    r = n - x + 1;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + 3 * n - 6 * r + 3 - y +
           r;
  }
  if (x >= y & x + y <= n + 1) {
    r = y;
    return 4 * (r - 1) * n - 4 * (r - 1) * (r - 1) + 1 + 4 * n - 8 * r + 4 - x +
           r;
  }
  return 0;
}

int f(int x, int y) {
  ll ans = ff(x, y);
  ll sum = 0;
  while (ans) {
    sum += ans % 10;
    ans /= 10;
  }
  return sum;
}

int main() {
  int T;
  scanf("%d", &T);
  while (T--) {
    int m, q;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= m; i++) {
      scanf("%d%d", &p[i].x, &p[i].y);
    }
    sort(p + 1, p + m + 1);
    build(1, n, root[0]);
    for (int i = 1; i <= m; i++) {
      update(1, n, root[i], root[i - 1], p[i].x, f(p[i].x, p[i].y));
    }
    while (q--) {
      point p1, p2;
      scanf("%d%d%d%d", &p1.x, &p1.y, &p2.x, &p2.y);
      int t1 = lower_bound(p + 1, p + m + 1, p1) - p - 1;
      int t2 = upper_bound(p + 1, p + m + 1, p2) - p - 1;
      printf("%d\n", query(1, n, root[t2], root[t1], p1.x, p2.x));
    }
  }
  return 0;
}