题目描述
现在有一堆数字共N个数字($N \leq 10^6$),以及一个大小为k的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
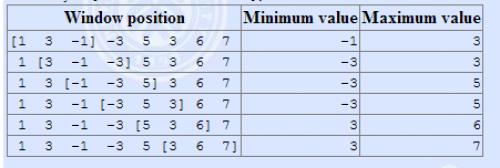
输入格式
输入一共有两行,第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入 #1
输出 #1
1
2
| -1 -3 -3 -3 3 3
3 3 5 5 6 7
|
说明/提示
50%的数据, $ n \leq 10^5 $
100%的数据,$ n \leq 10^6 $
前几天听肖大佬提到了单调队列,特来补题,不过似乎单调队列用的没有单调栈那么多:-)
思路:
维护两个单调的双端队列:
一个单调递增,该队列的最左端即为当前区间的最小元素。入队一个元素时,若队尾的元素>=当前元素,则它们对最小值毫无贡献,可直接弹出,直到队列为空或碰到比当前元素小的。然后队列左端也要把id不属于这个区间的弹出,之后更新答案
一个单调递减,该队列的最左端即为当前区间的最大元素。入队一个元素时,若队尾的元素<=当前元素,则它们对最大值毫无贡献,可直接弹出,直到队列为空或碰到比当前元素大的。然后队列左端也要把id不属于这个区间的弹出,之后更新答案。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int a[maxn];
int mina[maxn];
int maxa[maxn];
int main() {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
deque<int> q1, q2;
for (int i = 0; i < n; i++) {
if (q1.empty()) {
q1.push_back(i);
} else {
while (!q1.empty() && a[q1.back()] >= a[i]) {
q1.pop_back();
}
q1.push_back(i);
while (q1.front() <= i - k) {
q1.pop_front();
}
if (i >= k - 1) {
mina[i - k + 1] = q1.front();
}
}
if (q2.empty()) {
q2.push_back(i);
} else {
while (!q2.empty() && a[q2.back()] <= a[i]) {
q2.pop_back();
}
q2.push_back(i);
while (q2.front() <= i - k) {
q2.pop_front();
}
if (i >= k - 1) {
maxa[i - k + 1] = q2.front();
}
}
}
for (int i = 0; i < n - k + 1; i++) {
printf("%d ", a[mina[i]]);
}
printf("\n");
for (int i = 0; i < n - k + 1; i++) {
printf("%d ", a[maxa[i]]);
}
printf("\n");
return 0;
}
|

