时间限制：$2000ms$

空间限制：$256MB$

query

Given a permutation $p$ of length $n$, you are asked to answer $m$ queries, each query can be represented as a pair ($l,\ r$), you need to find the number of pair($i,\ j$) such that $l\le i < j\le r$ and $\min(p_i, p_j)=gcd(p_i, p_j)$.

Input

There is two integers $n$($1\le n\le 10^5$), $m$($1\le m\le 10^5$) in the first line, denoting the length of $p$ and the number of queries.

In the second line, there is a permutation of length $n$, denoting the given permutation $p$. It is guaranteed that $p$ is a permutation of length $n$.

For the next $m$ lines, each line contains two integer $l_i$ and $r_i$($1 \le l_i \le r_i \le n$), denoting each query.

Output

For each query, print a single line containing only one integer which denotes the number of pair($i,\ j$).

样例输入

1
2
3
4
3 2
1 2 3
1 3
2 3

样例输出

1
2
2
0

题意

给你一个 $n$ 的全排列，接下来有 $m$ 个查询，查询的是某个区间内有多少个数对($p_i,\ p_j$)($i<j$)，这些数对满足条件 $gcd(p_i, p_j) = \min(p_i, p_j)$， 也就是这两个数之间存在倍数关系。

解决方案

唉，比赛的时候一直认为这是个纯粹的数论题，没往数据结构上想……

这题有个非常重要的条件，就是这个数组是 $n$ 的全排列！这样你才能够在 $O(nlogn)$ 的时间复杂度内把所有的数对全部筛选出来。

首先，我们先把所有的数对筛选出来，注意是坐标($i, j$)，例如数组 $1,2,3,4,5$ ，先筛 $1$ 的，满足条件的数对是 ($1,2$)($1,3$)($1,4$)($1,5$)，注意，数对里的数是这些数的坐标，而不是数本身。之后，把 $2,3,4,5$ 放到编号为 $1$ 的 $vector$ 里面，然后以此类推，把每个数往后的满足条件的数对都求出来并放进对应的 $vector$ 里面。可以先看一下这部分代码，这个时间复杂度是：

括号项是调和级数，和为 $\ln n$ 。

接下来有两种做法，一种是主席树在线查询，一种是线段树离线查询，思路是一样的，这里只讲前一种做法（没学过主席树的话建议学一下）。

首先考虑主席树存储什么，题目求满足条件的数对的数量，考虑存储区间和，那么这个和是什么呢？这得先清楚这棵主席树的建树过程。我们顺序扫描，每扫描一个点，就把它对应的 $vector$ 里面的所有下标，去主席树更新一下，准确的讲是这一点的值要 +1，现在明白主席树存储什么了吧？对于叶子节点，就是这个下标所处的点，能够满足条件的数对的数量。这里之所以要用主席树，就是因为它满足前缀和的性质，查询 ($l, r$) 可以用区间 ($1, r$) - ($1, l-1$) 。

这题有个坑爹的地方，由于共有 $n\ln n$ 个数对，每个点不止更新一次，而是要把它对应的 $vector$ 里面的所有点都更新一下，所以空间复杂度不是常规主席树的 $O(n\log n)$ ，而是 $O(n\log^2n)$ ，空间上卡的很紧…… ，总共就给了 $256MB$ 的空间，博主用了 $250MB$ ……

1

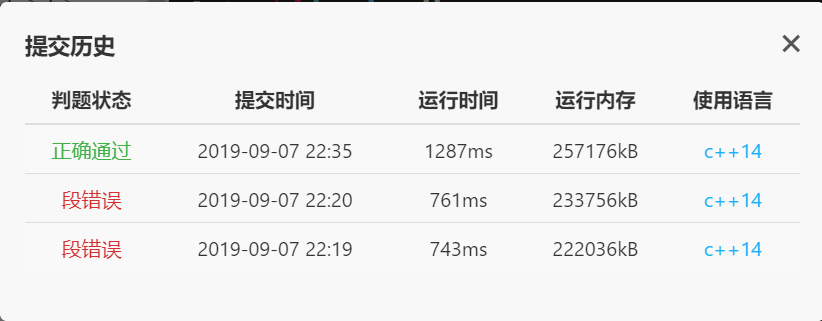
下面上代码

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn = 1e5 + 10;

struct node {
  int lch, rch, sum;
} tree[maxn * 210];

int a[maxn];
int p[maxn];
int root[maxn];
int tot;
vector<int> vt[maxn];

void build(int l, int r, int& rt) {
  rt = tot++;
  if (l == r) {
    return;
  }
  int m = (l + r) >> 1;
  build(l, m, tree[rt].lch);
  build(m + 1, r, tree[rt].rch);
}

void update(int l, int r, int& rt, int pre, int c) {
  rt = tot++;
  tree[rt] = tree[pre];
  tree[rt].sum++;
  if (l == r) {
    return;
  }
  int m = (l + r) >> 1;
  if (c <= m) {
    update(l, m, tree[rt].lch, tree[pre].lch, c);
  } else {
    update(m + 1, r, tree[rt].rch, tree[pre].rch, c);
  }
}

int query(int l, int r, int tl, int tr, int rt, int pre) {
  if (l <= tl && r >= tr) {
    return tree[rt].sum - tree[pre].sum;
  }
  int tm = (tl + tr) >> 1;
  int tmp = 0;
  if (l <= tm) {
    tmp += query(l, r, tl, tm, tree[rt].lch, tree[pre].lch);
  }
  if (r > tm) {
    tmp += query(l, r, tm + 1, tr, tree[rt].rch, tree[pre].rch);
  }
  return tmp;
}

int main() {
  int n, m;
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) {
    scanf("%d", &a[i]);
    p[a[i]] = i;
  }
  for (int i = 1; i <= n; i++) {
    for (int j = 2 * a[i]; j <= n; j += a[i]) {
      vt[i].push_back(p[j]);
    }
  }
  build(1, n, root[0]);
  for (int i = 1; i <= n; i++) {
    root[i] = root[i - 1];
    for (int j = 0; j < vt[i].size(); j++) {
      update(1, n, root[i], root[i], vt[i][j]);
    }
  }
  while (m--) {
    int l, r;
    scanf("%d%d", &l, &r);
    printf("%d\n", query(l, r, 1, n, root[r], root[l - 1]));
  }
  return 0;
}