Balance Scale

时间限制 : 8 sec

空间限制 : 262144 KB

题目链接

You, an experimental chemist, have a balance scale and a kit of weights for measuring weights of powder chemicals.

For work efficiency, a single use of the balance scale should be enough for measurement of each amount. You can use any number of weights at a time, placing them either on the balance plate opposite to the chemical or on the same plate with the chemical. For example, if you have two weights of 2 and 9 units, you can measure out not only 2 and 9 units of the chemical, but also 11 units by placing both on the plate opposite to the chemical (Fig. C-1 left), and 7 units by placing one of them on the plate with the chemical (Fig. C-1 right). These are the only amounts that can be measured out efficiently.

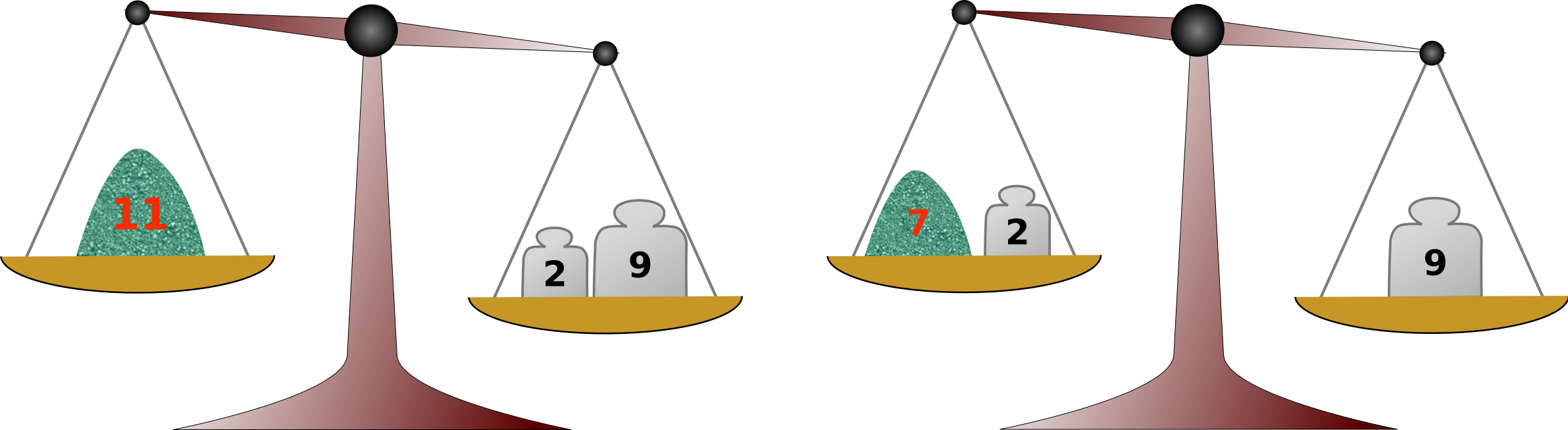imgFig. C-1 Measuring 11 and 7 units of chemical

You have at hand a list of amounts of chemicals to measure today. The weight kit already at hand, however, may not be enough to efficiently measure all the amounts in the measurement list. If not, you can purchase one single new weight to supplement the kit, but, as heavier weights are more expensive, you’d like to do with the lightest possible.

Note that, although weights of arbitrary positive masses are in the market, none with negative masses can be found.

Input

The input consists of at most 100 datasets, each in the following format.

n m
$a_1 a_2 … a_n$
$w_1 w_2 … w_n$

The first line of a dataset has $n$ and $m$, the number of amounts in the measurement list and the number of weights in the weight kit at hand, respectively. They are integers separated by a space satisfying $1\le n\le 100$ and $1\le m \le10$.

The next line has the $n$ amounts in the measurement list, $a_1$ through $a_n$ ，separated by spaces. Each of $a_i$ is an integer satisfying $1\le a_i \le 10^9$, and $a_i \ne a_j$ holds for $i \ne j$.

The third and final line of a dataset has the list of the masses of the $m$ weights at hand, $w_1$ through $w_m$，separated by spaces. Each of $w_i$ is an integer, satisfying $1\le w_i\le 10^8$. Two or more weights may have the same mass.

The end of the input is indicated by a line containing two zeros.

Output

For each dataset, output a single line containing an integer specified as follows.

  • If all the amounts in the measurement list can be measured out without any additional weights, $0$.
  • If adding one more weight will make all the amounts in the measurement list measurable, the mass of the lightest among such weights. The weight added may be heavier than $10^8$ units.
  • If adding one more weight is never enough to measure out all the amounts in the measurement list, $-1$.

Sample Input

1
2
3
4
5
6
7
8
9
10
11
12
13
4 2
9 2 7 11
2 9
6 2
7 3 6 12 16 9
2 9
5 2
7 3 6 12 17
2 9
7 5
15 21 33 48 51 75 111
36 54 57 93 113
0 0

Output for the Sample Input

1
2
3
4
0
5
-1
5

题意

给你一堆有一定重量的物品和砝码，每种砝码只能用一次，我们知道，把砝码放在天平两侧搭配可以称量不同重量的物品，现在问题来了，这些物品里有些是现有砝码无法称量的，让你添加一个砝码，使得所有物品都可以称量，且这个砝码的重量最小。若存在这么一个砝码，输出其重量，否则输出-1

解决方案

数据量很小，直接3进制枚举每一种砝码的摆放情况，从而得出每一种物品可接受的砝码，然后取不同物品可取砝码的交的最小值。

此题巨坑，卡常卡到自闭，和STL有关的，除了sort基本在此题都无法使用（石油大学OJ，原OJ不卡常）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
/**
 * cnm,卡常的巅峰之作.
 *
 */

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int a[100 + 10];
int w[100 + 10];
int vt[110];
int num_st[110];
ll st[110][60000];

int intersection(int s, int u) {
  int i = 0, j = 0;
  int num = 0;
  while (i < num_st[s] && j < num_st[u]) {
    while (i < num_st[s] && st[s][i] < st[u][j]) {
      i++;
    }
    while (j < num_st[u] && st[u][j] < st[s][i]) {
      j++;
    }
    if (i < num_st[s] && j < num_st[u] && st[s][i] == st[u][j]) {
      st[s][num++] = st[s][i];
      i++;
      j++;
    }
  }
  return num;
}

int main() {
  int n, m;
  // freopen("in.txt", "r", stdin);
  while (scanf("%d%d", &n, &m) && (n || m)) {
    int wr = 0;
    memset(num_st, 0, sizeof(num_st));
    for (int i = 0; i < n; i++) {
      scanf("%d", &a[i]);
    }
    for (int i = 0; i < m; i++) {
      scanf("%d", &w[i]);
    }
    int tot = pow(3, m);
    ll we[tot + 10];
    for (int i = 0; i < tot; i++) {
      int t = i;
      ll num = 0;
      for (int j = 0; j < m; j++) {
        if (t % 3 == 1) {
          num += w[j];
        } else if (t % 3 == 2) {
          num -= w[j];
        }
        t /= 3;
      }
      we[i] = num;
    }
    for (int i = 0; i < n; i++) {
      int flag = 0;
      for (int j = 0; j < tot; j++) {
        if (a[i] == abs(we[j])) {
          flag = 1;
          break;
        }
      }
      if (!flag) {
        vt[wr++] = i;
        st[i][num_st[i]++] = a[i];
      }
    }
    if (!wr) {
      printf("0\n");
      continue;
    }
    for (int i = 0; i < wr; i++) {
      int u = vt[i];
      for (int j = 0; j < tot; j++) {
        st[u][num_st[u]++] = abs(we[j] - a[u]);
      }
      sort(st[u], st[u] + num_st[u]);
      num_st[u] = unique(st[u], st[u] + num_st[u]) - st[u];
    }
    int s = vt[0];
    for (int i = 1; i < wr; i++) {
      int u = vt[i];
      num_st[s] = intersection(s, u);
      if (!num_st[s]) {
        break;
      }
    }
    if (!num_st[s]) {
      printf("-1\n");
    } else {
      printf("%lld\n", st[s][0]);
    }
  }
  return 0;
}